006. 삼각형의 넓이 공식

 

 

삼각형의 넓이 공식 소개

$S$ $=$ $\dfrac{1}{2}ah$ ( $S$ : 삼각형의 넓이 )

삼각형의 넓이 공식의 증명을 위해 '단위길이', '단위정사각형', '단위넓이', '직사각형의 넓이'에 대해 먼저 알아봅시다.

 

단위길이, 단위정사각형, 단위넓이

한 변의 길이가 단위길이, 즉 1인 정사각형을 단위정사각형이라고 하고, 단위정사각형의 넓이를 단위넓이라고 한다. 단위길이와 마찬가지로 단위넓이를 1로 정의한다.

 

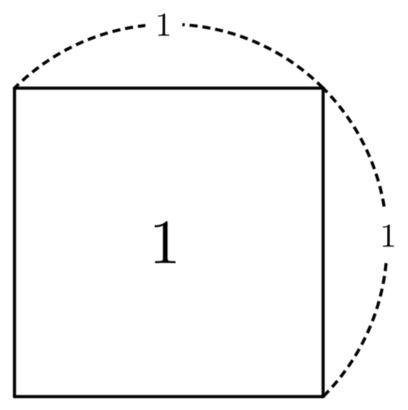
직사각형의 넓이

가로의 길이가 4, 세로의 길이가 3인 직사각형에 대하여

가로, 세로가 모두 1인 단위정사각형으로 나누면

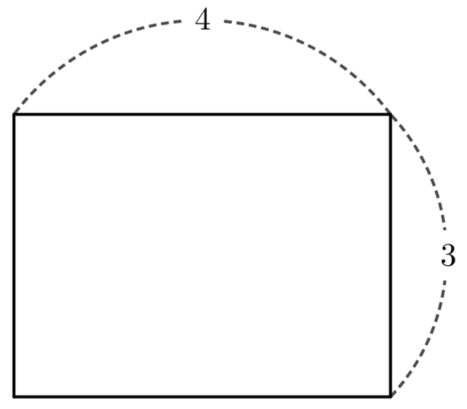
12개의 단위정사각형이 나오므로 직사각형의 넓이는 12이다.

직사각형의 넓이를 구할 때, 단위정사각형의 개수를 세는 것보다

 

(가로의 길이)$\times$(세로의 길이)

 

를 이용하면 직사각형을 단위정사각형으로 나눌 필요 없이 직사각형의 넓이를 빠르게 구할 수 있다.

따라서

 

(직사각형의 넓이)$=$(가로의 길이)$\times$(세로의 길이)

 

이 '직사각형의 넓이'를 이용하여 삼각형의 넓이 공식을 다음과 같이 구할 수 있습니다.

 

삼각형의 넓이 공식 증명

(i) 예각삼각형의 넓이 구하기

예각삼각형 $\rm{ABC}$의 넓이를 구하기 위해 점 $\rm{A}$에서 선분 $\rm{BC}$에 수선의 발을 내리고,

이를 이용해 삼각형 $\rm{ABC}$를 그림과 같이 파란색 직각삼각형과 보라색 직각삼각형으로 나눈다.

파란색, 보라색 직각삼각형과 합동인 빨간색 직각삼각형, 주황색 직각삼각형을 만들어 빗변에 붙이면 그림과 같은 직사각형이 된다.

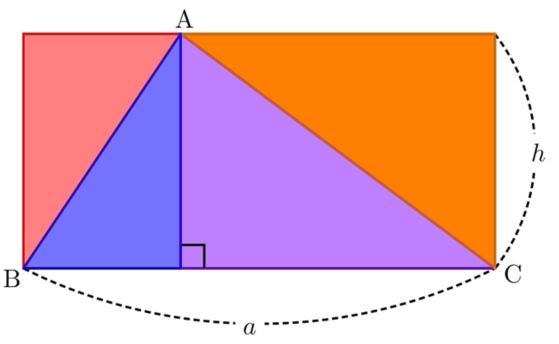
$\qquad$ $\qquad$ (직사각형의 넓이) $=$ (가로의 길이) $\times$ (세로의 길이) $=$ $a \times h$ $=ah$

이므로

$\qquad$ $\qquad$ (삼각형의 넓이) $=$ $\dfrac{1}{2}$ $\times$ (직사각형의 넓이) $=$ $\dfrac{1}{2}$ $ a h$

따라서

$\qquad$ $\qquad$ (삼각형의 넓이) $=$ $S$ $=$ $\dfrac{1}{2} a h$

 

(ii) 둔각삼각형의 넓이 구하기

그림과 같은 $\angle$$\rm{B}$가 둔각인 둔각삼각형 $\rm{ABC}$의 넓이를 구하자.

 

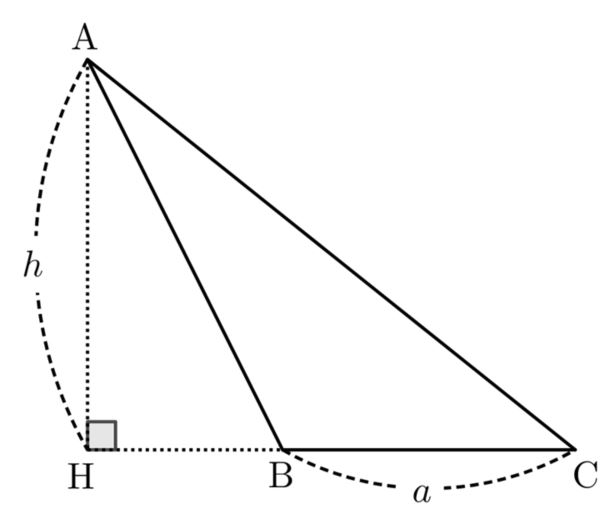
점 $\rm{A}$에서 직선 $\rm{BC}$에 내린 수선의 발을 $\rm{H}$라 하고, $\overline{\rm{HB}}$ $=$ $b$라 하자.

 

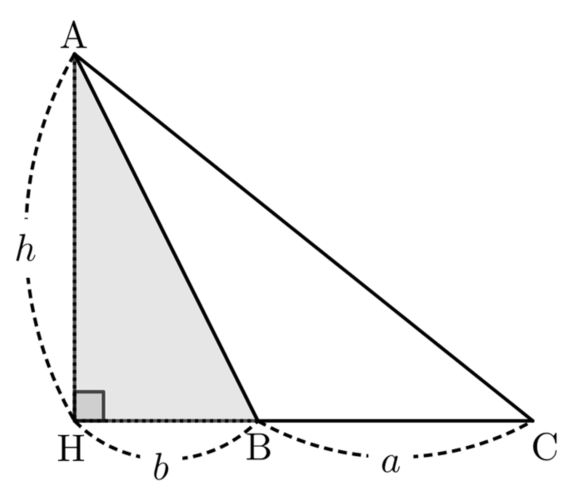
$\qquad$ $\qquad$ (삼각형의 넓이) $=$ (삼각형 $\rm{AHC}$의 넓이) $-$ (삼각형 $\rm{AHB}$의 넓이)

이고, 예각삼각형의 넓이 공식에 의해

$\qquad$ $\qquad$ (삼각형의 넓이) $=$ $\dfrac{1}{2}(a+b)h$ $-$ $\dfrac{1}{2}bh$ $=$ $\dfrac{1}{2}$ $ a h$

따라서

$\qquad$ $\qquad$ (삼각형의 넓이)$ = S = \dfrac{1}{2} a h$