014. 삼각형의 중선정리
193개 수학 공식 증명 2024. 5. 23. 17:30중선정리 소개
| 삼각형 $\rm{ABC}$와 중선 $\overline{\rm{AM}}$에 대하여 $\overline{\rm{AB}}^2+\overline{\rm{AC}}^2=2 \left( \overline{\rm{AM}}^2 + \overline{\rm{BM}}^2 \right) $ |
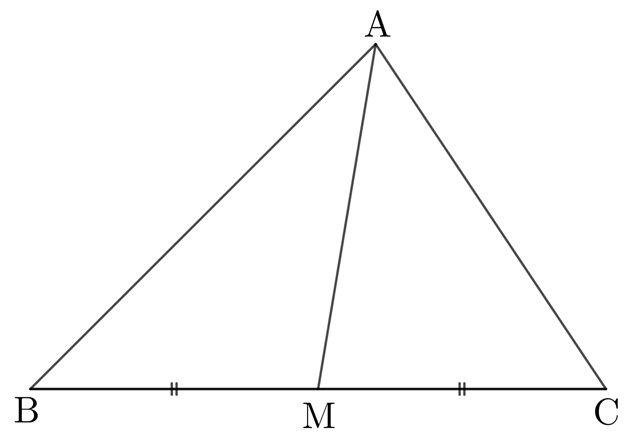 |
중선정리는 다음 세 가지 방법을 이용해 증명할 수 있습니다.
$\qquad$ ① 좌표평면과 두 점 사이의 거리 공식 이용하는 방법
$\qquad$ ② 코사인법칙을 이용하는 방법
$\qquad$ ③ 피타고라스의 정리를 이용하는 방법
증명① - 좌표평면과 두 점사이의 거리 공식을 이용하는 방법
그림과 같이 삼각형 $\rm{ABC}$에 대하여 변 $\rm{BC}$가 $x$축 위에 있고, 중점 $\rm{M}$이 원점에 위치 하도록 좌표평면 위로 옮긴다. 그리고 점 $\rm{C}$의 좌표를 $(c, 0)$, 점 $\rm{A}$의 좌표를 $(a,b)$라 하자.
이때 점 $\rm{M}$이 변 $\rm{BC}$의 중점이므로 점 $\rm{B}$의 좌표는 $(-c,0)$이다.

두 점 사이의 거리 공식에 의해
$\qquad$ $\overline{\rm{AB}}$ $=$ $\sqrt{ \left\{ a- (-c) \right\}^{2} + b^{2}}$
$\qquad$ $\overline{\rm{AC}}$ $=$ $\sqrt{ \left( a- c \right)^{2} + b^{2}}$
$\qquad$ $\overline{\rm{AM}}$ $=$ $\sqrt{ a^2 + b^{2}}$
$\qquad$ $\overline{\rm{BM}}$ $=$ $c$
이므로
$\qquad$ (좌변) $=$ $\overline{\rm{AB}}^2+\overline{\rm{AC}}^2$
$\qquad$ $\qquad$ $=$ $ \left\{ a- (-c) \right\}^{2} + b^{2} + \left( a- c \right)^{2} + b^{2}$
$\qquad$ $\qquad$ $=$ $2a^2 + 2b^2 + 2c^2$
$\qquad$ (우변) $=$ $ 2 \left( \overline{\rm{AM}}^2 + \overline{\rm{BM}}^2 \right)$
$\qquad$ $\qquad$ $=$ $2a^2 + 2b^2 + 2c^2$
이다. 즉,
$\qquad$ $\overline{\rm{AB}}^2+\overline{\rm{AC}}^2=2 \left( \overline{\rm{AM}}^2 + \overline{\rm{BM}}^2 \right) $
증명② - 코사인법칙을 이용하는 방법
삼각형 $\rm{ABC}$에 대하여 그림과 같이
$\qquad$ $\angle \rm{AMB} = \theta_{1}$, $\angle \rm{AMC} = \theta_{2}$
라 하자.

코사인법칙에 의해
$\qquad$ $\overline{\rm{AB}}^2 = \overline{\rm{AM}}^2 + \overline{\rm{BM}}^2 - 2 \overline{\rm{AM}}$ $ \overline{\rm{BM}} \cos{\theta_{1}}$
$\qquad$ $\overline{\rm{AC}}^2 = \overline{\rm{AM}}^2 + \overline{\rm{CM}}^2 - 2 \overline{\rm{AM}}$ $ \overline{\rm{CM}} \cos{\theta_{2}}$
이다. $\overline{\rm{BM}}$ $=$ $\overline{\rm{CM}}$이고 $\theta_{2} = \pi - \theta_{1}$이므로
$\qquad$ $\overline{\rm{AB}}^2 = \overline{\rm{AM}}^2 + \overline{\rm{BM}}^2 - 2 \overline{\rm{AM}}$ $ \overline{\rm{BM}} \cos{\theta_{1}}$
$\qquad$ $\overline{\rm{AC}}^2 = \overline{\rm{AM}}^2 + \overline{\rm{BM}}^2 - 2 \overline{\rm{AM}}$ $ \overline{\rm{BM}} ( \cos{\pi - \theta_{1}} )$
이다. 즉,
$\qquad$ $\overline{\rm{AB}}^2 = \overline{\rm{AM}}^2 + \overline{\rm{BM}}^2 - 2 \overline{\rm{AM}}$ $ \overline{\rm{BM}} \cos{\theta_{1}}$
$\qquad$ $\overline{\rm{AC}}^2 = \overline{\rm{AM}}^2 + \overline{\rm{BM}}^2 + 2 \overline{\rm{AM}}$ $ \overline{\rm{BM}} \cos{\theta_{1}}$
이므로
$\qquad$ $\overline{\rm{AB}}^2+\overline{\rm{AC}}^2=2 \left( \overline{\rm{AM}}^2 + \overline{\rm{BM}}^2 \right) $
증명③ - 피타고라스의 정리를 이용하는 방법
삼각형 $\rm{ABC}$에 대하여 꼭짓점 $\rm{A}$에서 변 $\rm{BC}$에 내린 수선의 발을 $\rm{H}$라 하자.
피타고라스의 정리에 의해 직각삼각형 $\rm{AHB}$, $\rm{AHC}$, $\rm{AHM}$에서

$\qquad$ $\overline{\rm{AB}}^2 = \overline{\rm{AH}}^2 + \overline{\rm{BH}}^2$ ……ⓐ
$\qquad$ $\overline{\rm{AC}}^2 = \overline{\rm{AH}}^2 + \overline{\rm{CH}}^2$ ……ⓑ
$\qquad$ $\overline{\rm{AM}}^2 = \overline{\rm{AH}}^2 + \overline{\rm{MH}}^2$ ……ⓒ
이다. 한편
$\qquad$ $\overline{\rm{BH}} = \overline{\rm{BM}} + \overline{\rm{MH}}$ ……ⓓ
$\qquad$ $\overline{\rm{CH}} = \overline{\rm{CM}} + \overline{\rm{MH}} = \overline{\rm{BH}} - \overline{\rm{MH}}$ ……ⓔ
이므로 ⓓ를 ⓐ에 대입, ⓔ를 ⓑ에 대입하면
$\qquad$ $\overline{\rm{AB}}^2 = \overline{\rm{AH}}^2 + \left( \overline{\rm{BM}} + \overline{\rm{MH}} \right)^2$
$\qquad$ $\overline{\rm{AC}}^2 = \overline{\rm{AH}}^2 + \left( \overline{\rm{BM}} - \overline{\rm{MH}} \right)^2$
이다. 이 등식을 변끼리 각각 더하면
$\qquad$ $ \overline{\rm{AB}}^2 + \overline{\rm{AC}}^2 = 2 \overline{\rm{AH}}^2 + 2 \overline{\rm{BM}}^2 + \overline{\rm{MH}}^2$ ……ⓕ
이다. ⓕ에 ⓒ를 이용하여 식을 바꾸면
$\qquad$ $\overline{\rm{AB}}^2+\overline{\rm{AC}}^2=2 \left( \overline{\rm{AM}}^2 + \overline{\rm{BM}}^2 \right) $
'193개 수학 공식 증명' 카테고리의 다른 글
| 015. 정사각형의 넓이 공식 (0) | 2024.05.27 |
|---|---|
| 013. 무게중심 공식 (0) | 2024.05.21 |
| 012. 사선 공식 (0) | 2024.05.02 |
| 011. 두 벡터가 생성하는 삼각형의 넓이 공식 (0) | 2024.04.26 |
| 010. 외접원과 삼각형의 넓이 공식 (0) | 2024.04.23 |







